ForagerNet3_Demography (Version 3)
Blog Posts
- ForagerNet3_Demography (Version 3): Description and Code Available (11/29/2016)
- Three-Headed Research Monster: A Brief Update (9/8/2016)
- Memory Leak Plugged, FN3_D_V3 Model Performing Again (3/30/2016)
- Friday Digest: Fringe Utopia, Memory Leaks, the Sword, and an Open Invitation to "The Walking Dead" (3/25/2016)
- Repast Simphony: There's Light at the End of the Tunnel (3/18/2016)
The ForagerNet3_Demography model (Version 3) is a non-spatial ABM designed to serve as a platform for exploring several aspects of hunter-gatherer demography:
Other than being implemented in Repast Simphony rather than Repast J, this model is identical to the model was used by White (2016).
- How demographically-relevant behaviors at the person- and household-levels are related to one another;
- How those lower-level behaviors are related to the system-level demographic characteristics of living populations;
- How the “paleodemographic” characteristics of assemblages of dead individuals are related to the demographic characteristics of the living population from which those assemblages were drawn.
Other than being implemented in Repast Simphony rather than Repast J, this model is identical to the model was used by White (2016).
This page provides documentation and the raw code for FN3D_V3. The following files are available for download:
- Description (pdf file; same content as on this page)
- Java files written for implementation of the model in Repast Simphony:
Overview
The FN3D_V3 model has three main levels: person, household, and system. Inter-related person- and household-level methods represent birth, death, and the creation/dissolution of male-female pair bonds (note: the terms “pair bond” and “marriage” are used inter-changeably in this description and denote the same behavior in the model). These methods and their inter-relationships were informed by data from ethnographic hunter-gatherers. Many parameters in the model are continuously variable, allowing the model to be used to “sweep” through a range of values and observe how differences in parameters are related to model behavior. The dependency ratio (the ratio of consumers to producers in a household) is a key variable in many economic decisions embedded in the methods.
This model is not intended to represent all details of any particular hunter-gatherer system. The exclusion of extraneous detail is a purposeful strategy to aid in constructing a model whose structure and behavior are understandable. The representations in the model are generic and broadly applicable to a variety of hunter-gatherer systems. In the terminology of Gilbert (2008), FN3D_V3 is a “middle range” model. Middle range models “aim to describe the characteristics of a particular social phenomenon, but in a sufficiently general way that their conclusions can be applied” to many examples of the same phenomenon (Gilbert 2008:42).
FN3D_V3 is an altered version of the FN3D_V2 model described by White (2014).
FN3D_V3 was built using Repast Simphony. Repast (Recursive Porous Agent Simulation Toolkit) is a free, open-source agent-based modeling and simulation toolkit that was created at the University of Chicago in collaboration with Argonne National Laboratory. Documentation of Repast can be found at www.repast.sourceforge.net.
The code for the model is supplied in the Java files that are read by Repast Simphony: ForagerNet3Builder.java; Household.java; Link.java; Model.java; and Person.java.
The first section of this guide provides a description of the representations of time and the entities (persons, households, social links) in the model and a very brief overview of the major groups of methods in the model (pair bond, reproduction, and mortality). The second section describes model-level variables, parameters, and lists. The third section describes the “rules” and the operations of the model in detail with specific reference to sections of code.
This model is not intended to represent all details of any particular hunter-gatherer system. The exclusion of extraneous detail is a purposeful strategy to aid in constructing a model whose structure and behavior are understandable. The representations in the model are generic and broadly applicable to a variety of hunter-gatherer systems. In the terminology of Gilbert (2008), FN3D_V3 is a “middle range” model. Middle range models “aim to describe the characteristics of a particular social phenomenon, but in a sufficiently general way that their conclusions can be applied” to many examples of the same phenomenon (Gilbert 2008:42).
FN3D_V3 is an altered version of the FN3D_V2 model described by White (2014).
FN3D_V3 was built using Repast Simphony. Repast (Recursive Porous Agent Simulation Toolkit) is a free, open-source agent-based modeling and simulation toolkit that was created at the University of Chicago in collaboration with Argonne National Laboratory. Documentation of Repast can be found at www.repast.sourceforge.net.
The code for the model is supplied in the Java files that are read by Repast Simphony: ForagerNet3Builder.java; Household.java; Link.java; Model.java; and Person.java.
The first section of this guide provides a description of the representations of time and the entities (persons, households, social links) in the model and a very brief overview of the major groups of methods in the model (pair bond, reproduction, and mortality). The second section describes model-level variables, parameters, and lists. The third section describes the “rules” and the operations of the model in detail with specific reference to sections of code.
Representations in the Model
Time
Time passes in the model in the form of discrete steps, each representing one week (5200 steps representing 100 years). A week was chosen as the fundamental unit of time to allow representation of differences in the duration of gestational periods, post partum amenorrhea, and other variables relevant to reproduction and demography.
The model maintains a “seasonal clock” that resets to 1 at the beginning of every 52-step cycle. This clock is used to increment the ages of persons and households on a yearly basis.
Persons
Each agent in the model represents an individual person. An initial population of persons is created at the start of a model run. All subsequent persons are created through procreation.
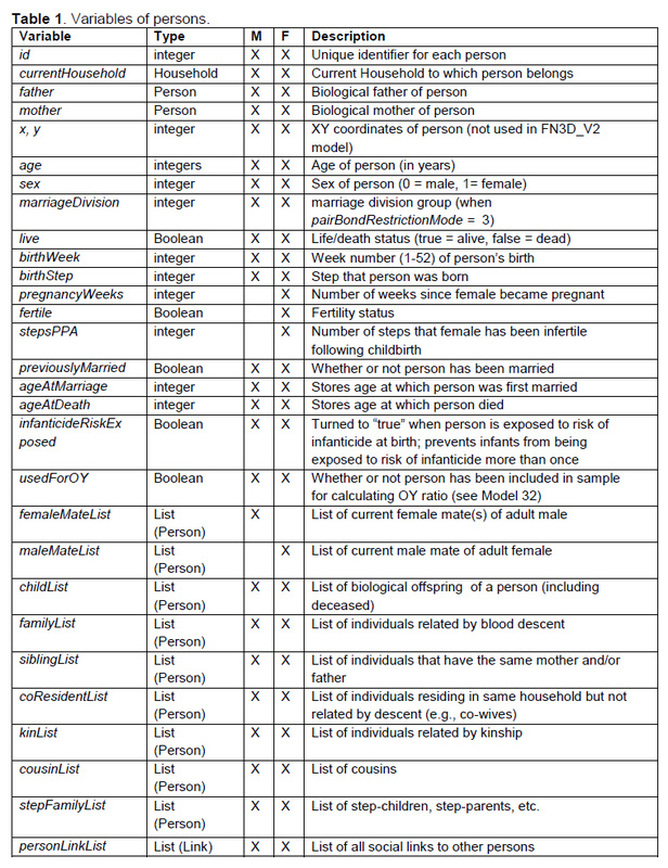
The variables and lists that are associated with each person are summarized in Table 1. Each person has variables to store his/her age and sex, variables to track various statuses (live/dead, household to which the person currently belongs, fertile/not fertile, etc.) and status changes (age at death, age at marriage), and various lists to store the identities of mates, persons related by descent (grandparents, parents, siblings, half-siblings, children), persons related by “kinship” (e.g., wife’s mother, wife’s father), and persons related through co-residence in a household unit. Each person has a list to store the identities of each social link that he/she has to another person in the world.
Time passes in the model in the form of discrete steps, each representing one week (5200 steps representing 100 years). A week was chosen as the fundamental unit of time to allow representation of differences in the duration of gestational periods, post partum amenorrhea, and other variables relevant to reproduction and demography.
The model maintains a “seasonal clock” that resets to 1 at the beginning of every 52-step cycle. This clock is used to increment the ages of persons and households on a yearly basis.
Persons
Each agent in the model represents an individual person. An initial population of persons is created at the start of a model run. All subsequent persons are created through procreation.
The variables and lists that are associated with each person are summarized in Table 1. Each person has variables to store his/her age and sex, variables to track various statuses (live/dead, household to which the person currently belongs, fertile/not fertile, etc.) and status changes (age at death, age at marriage), and various lists to store the identities of mates, persons related by descent (grandparents, parents, siblings, half-siblings, children), persons related by “kinship” (e.g., wife’s mother, wife’s father), and persons related through co-residence in a household unit. Each person has a list to store the identities of each social link that he/she has to another person in the world.
Households
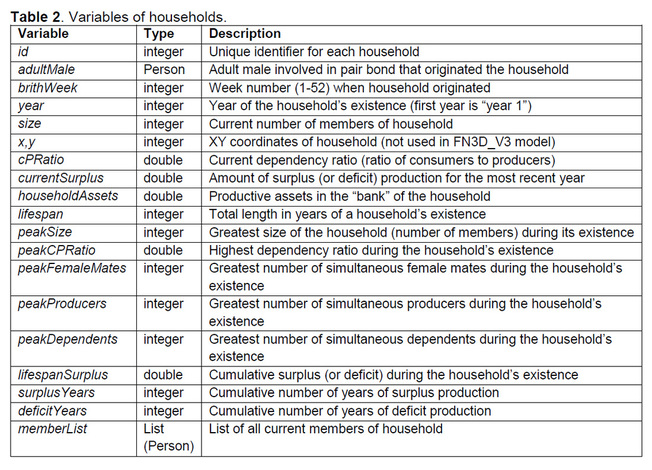
Households are co-residential groupings that are comprised mainly of persons related through affinity, descent, or marriage to a common partner (in the case of polygyny). A new household is created through a pair bond between a male and a female. The size and composition of a household may change by three main mechanisms: pair bonds, procreation, and mortality. The dependency ratio of a household (ratio of the number of consumers to the number of producers, aka the CP ratio) is a key factor in probability-based, household-level decisions in all three areas. The variables and lists associated with each household are summarized in Table 2.
Households are co-residential groupings that are comprised mainly of persons related through affinity, descent, or marriage to a common partner (in the case of polygyny). A new household is created through a pair bond between a male and a female. The size and composition of a household may change by three main mechanisms: pair bonds, procreation, and mortality. The dependency ratio of a household (ratio of the number of consumers to the number of producers, aka the CP ratio) is a key factor in probability-based, household-level decisions in all three areas. The variables and lists associated with each household are summarized in Table 2.
Social Links
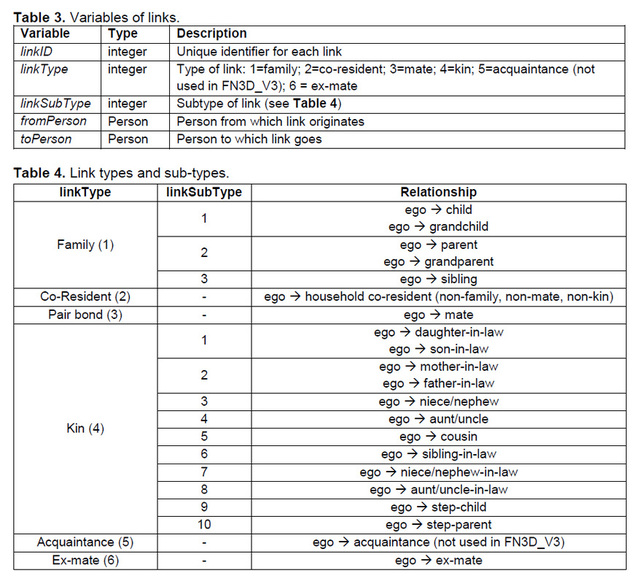
Social links are ties between pairs of living persons that define the nature of their relationship. Links are formed based on relationships of descent (family links), co-residence in a household (co-resident links), marriage (marriage links), and kinship (kin links). Family links indicate a consanguineal (i.e., blood descent) relationship. Kinship links are links of affinity (i.e., created through a pair bond). Co-resident links are established between individuals that co-reside in a household but qualify for neither family nor kin status as defined here. Variables associated with links are summarized in Table 3. Link types and sub-types are described in Table 4.
Social links are ties between pairs of living persons that define the nature of their relationship. Links are formed based on relationships of descent (family links), co-residence in a household (co-resident links), marriage (marriage links), and kinship (kin links). Family links indicate a consanguineal (i.e., blood descent) relationship. Kinship links are links of affinity (i.e., created through a pair bond). Co-resident links are established between individuals that co-reside in a household but qualify for neither family nor kin status as defined here. Variables associated with links are summarized in Table 3. Link types and sub-types are described in Table 4.
The creation of a social relationship between two people (e.g., Person 1 and Person 2) results in the creation of two uni-directional links: Person 1 --> Person 2 and Person 2 --> Person 1. This allows the relationship between Person 1 and Person 2 to be asymmetrical. There are always twice as many social links as there are social relationships between people.
There can only be one pair of links defining the relationship between any two people, and each of the links in this pair must be of the same class. It is impossible, for example, for the link from Person 1 to Person 2 to be a family link while the link from Person 2 to Person 1 is a kin link. Links are created or changed to the appropriate type when individuals are born, married, or change household. A change in the nature of the relationship between two persons will trigger a change in the class of the links that connect the two persons. Pairs of social links are dissolved as a result of the death of one of the persons.
In the model, social links are used mainly to restrict marriage between pairs of individuals. Various kinds of marriage restrictions can be represented in the model (see below).
Pair Bond Methods
Creation of male-female pair bonds (i.e., “marriages”) is the mechanism of household formation and one of the mechanisms (along with mortality and reproduction) for changing the size and composition of a household. A pair bond must be present for a female to become pregnant. In the current version of the FN3D_V3 model, females may have only a single male mate while males can have multiple female mates if polygyny is permitted by the model settings. This structural asymmetry allows the forms of pair-bonding that are most commonly found in hunter-gatherer societies.
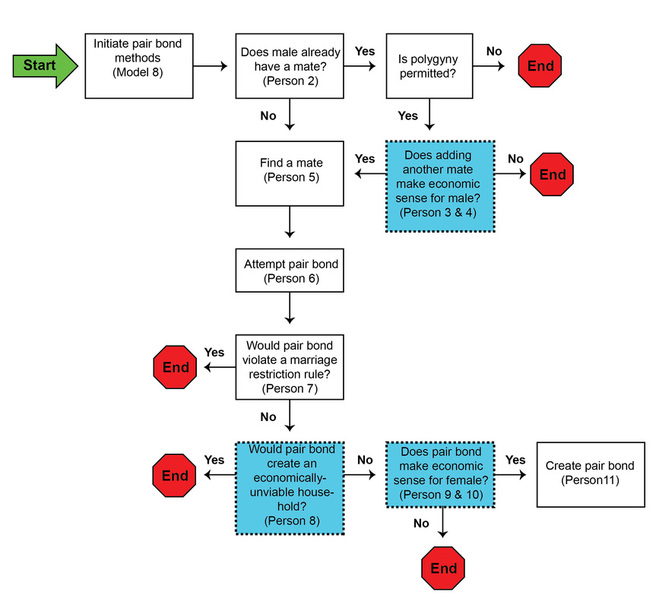
A schematic of the pair bond methods is shown in Figure 1. The numeric designations refer to sections of model code and the narrative descriptions of those sections provided below.
Each adult male will begin the pair bond methods at each step. Males and females each perform a sequence of probabilistic economic calculations that affect decisions to establish a new pair bond. Portions of the pair bond methods where the dependency ratio may be a factor are shown in blue boxes with dashed outlines in Figure 1. The weight of the dependency ratio (the ratio of consumers to producers within a household) in these calculations can be varied. If the male is already married and polygyny is permitted, the male calculation is based on the economic utility of adding an additional mate to his existing household. The female calculation is based on a comparison between the dependency ratio in her current household and the dependency ratio of the household she would join (e.g., as a second wife) or form with the male.
The model contains provisions for enforcing marriage prohibitions based on the kind of social relationship that exists between two individuals. Instability in pair bonds is also represented.
There can only be one pair of links defining the relationship between any two people, and each of the links in this pair must be of the same class. It is impossible, for example, for the link from Person 1 to Person 2 to be a family link while the link from Person 2 to Person 1 is a kin link. Links are created or changed to the appropriate type when individuals are born, married, or change household. A change in the nature of the relationship between two persons will trigger a change in the class of the links that connect the two persons. Pairs of social links are dissolved as a result of the death of one of the persons.
In the model, social links are used mainly to restrict marriage between pairs of individuals. Various kinds of marriage restrictions can be represented in the model (see below).
Pair Bond Methods
Creation of male-female pair bonds (i.e., “marriages”) is the mechanism of household formation and one of the mechanisms (along with mortality and reproduction) for changing the size and composition of a household. A pair bond must be present for a female to become pregnant. In the current version of the FN3D_V3 model, females may have only a single male mate while males can have multiple female mates if polygyny is permitted by the model settings. This structural asymmetry allows the forms of pair-bonding that are most commonly found in hunter-gatherer societies.
A schematic of the pair bond methods is shown in Figure 1. The numeric designations refer to sections of model code and the narrative descriptions of those sections provided below.
Each adult male will begin the pair bond methods at each step. Males and females each perform a sequence of probabilistic economic calculations that affect decisions to establish a new pair bond. Portions of the pair bond methods where the dependency ratio may be a factor are shown in blue boxes with dashed outlines in Figure 1. The weight of the dependency ratio (the ratio of consumers to producers within a household) in these calculations can be varied. If the male is already married and polygyny is permitted, the male calculation is based on the economic utility of adding an additional mate to his existing household. The female calculation is based on a comparison between the dependency ratio in her current household and the dependency ratio of the household she would join (e.g., as a second wife) or form with the male.
The model contains provisions for enforcing marriage prohibitions based on the kind of social relationship that exists between two individuals. Instability in pair bonds is also represented.
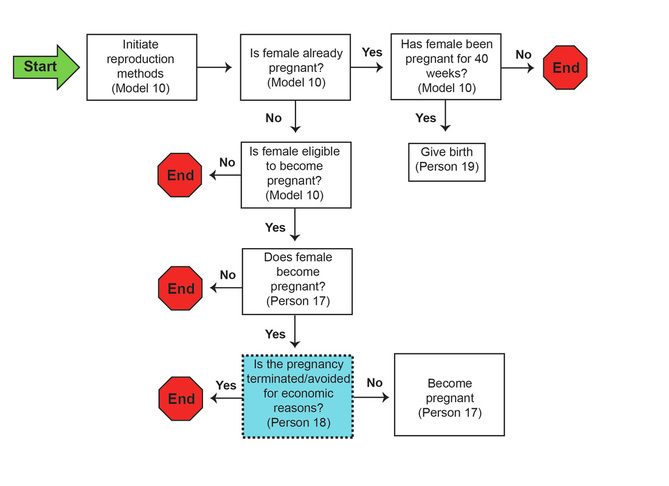
Reproduction Methods
A schematic of the reproduction methods is shown in Figure 2. The numeric designations refer to sections of model code and the narrative descriptions of those sections provided below.
Only females in a pair bond can become pregnant. Base probabilities of becoming pregnant are age-specific. Fertility is affected by the pattern of age-specific pregnancy probabilities defined in the model, a model-level parameter that globally adjusts probabilities of becoming pregnant, a period of post-partum amenorrhea, and economic decisions made at the household level. When a female is fertile, the base probability of becoming pregnant is adjusted by a calculation that considers how the addition of a child would affect the current dependency ratio of the female’s household. The probability of reproduction can be lowered (but not raised) by this calculation.
A schematic of the reproduction methods is shown in Figure 2. The numeric designations refer to sections of model code and the narrative descriptions of those sections provided below.
Only females in a pair bond can become pregnant. Base probabilities of becoming pregnant are age-specific. Fertility is affected by the pattern of age-specific pregnancy probabilities defined in the model, a model-level parameter that globally adjusts probabilities of becoming pregnant, a period of post-partum amenorrhea, and economic decisions made at the household level. When a female is fertile, the base probability of becoming pregnant is adjusted by a calculation that considers how the addition of a child would affect the current dependency ratio of the female’s household. The probability of reproduction can be lowered (but not raised) by this calculation.
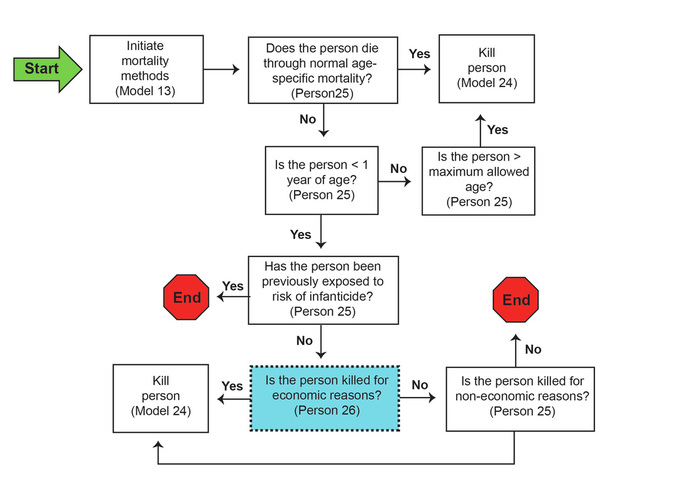
Mortality Methods
A schematic of the mortality methods is shown in Figure 3. The numeric designations refer to sections of model code and the narrative descriptions of those sections provided below.
Each person is exposed to a risk of death at each step. If a person reaches a maximum age set in the model, death is automatic. Below this maximum age, the base probability of a person dying is determined by an age-specific mortality rate. These rates are adjustable both through a model-level parameter and through a mechanism that adjusts mortality based on population size. Newborn infants may be exposed to an additional risk of death through the economically-sensitive infanticide mechanism that is represented in the model.
A schematic of the mortality methods is shown in Figure 3. The numeric designations refer to sections of model code and the narrative descriptions of those sections provided below.
Each person is exposed to a risk of death at each step. If a person reaches a maximum age set in the model, death is automatic. Below this maximum age, the base probability of a person dying is determined by an age-specific mortality rate. These rates are adjustable both through a model-level parameter and through a mechanism that adjusts mortality based on population size. Newborn infants may be exposed to an additional risk of death through the economically-sensitive infanticide mechanism that is represented in the model.
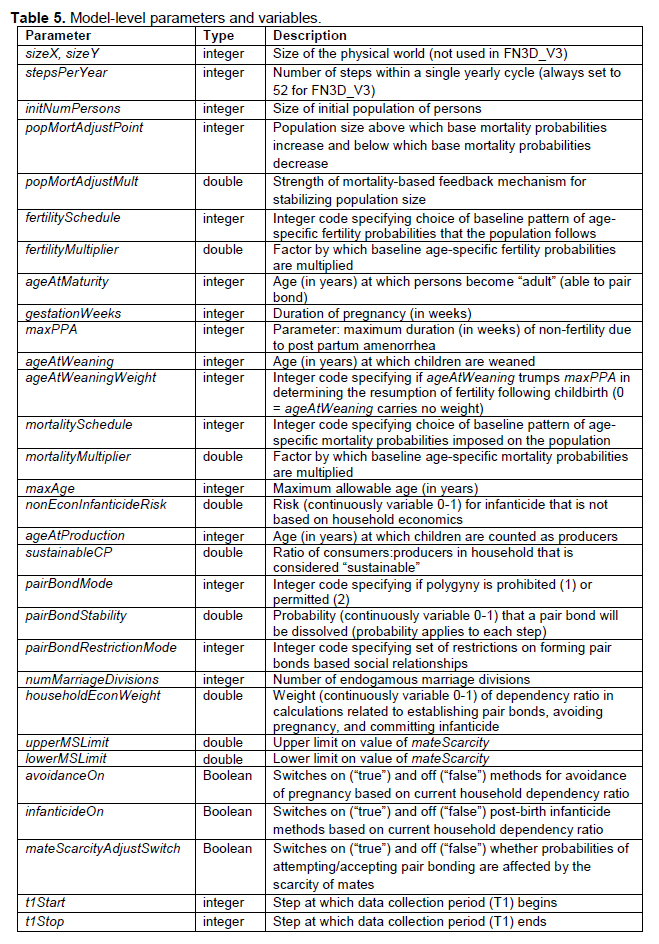
Model-Level Parameters, Variables, and Lists
Model-level parameters establish values for key aspects of the system. The values of these parameters do not change as a result of the dynamics of the model, but can be changed or randomized as part of an experiment. Model-level parameters are described in Table 5.
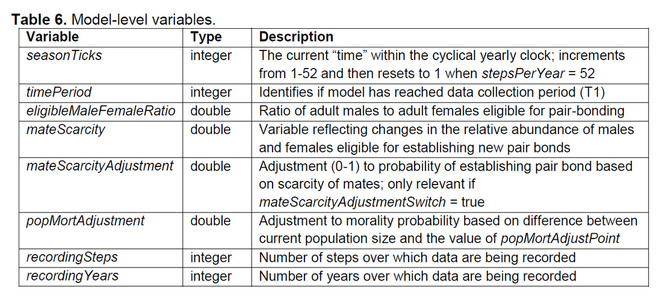
Model-level variables are measures that change as a result of operations, behaviors, or the passage of time during a model run. Model-level variables are listed in Table 6.
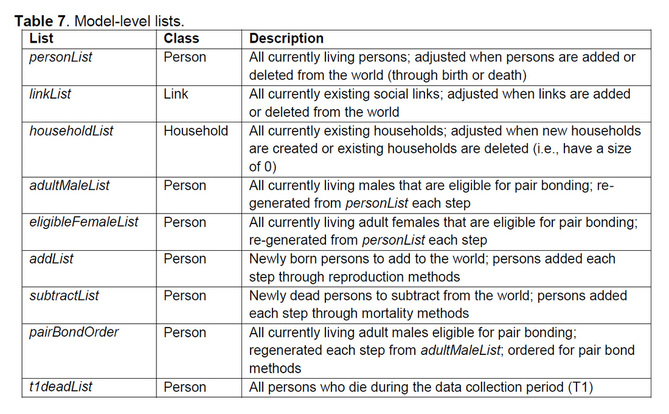
Model-level lists are used to hold the identities of the individual entities that exist in the world during a run. These lists are updated throughout a run. Model-level lists are described in Table 7.
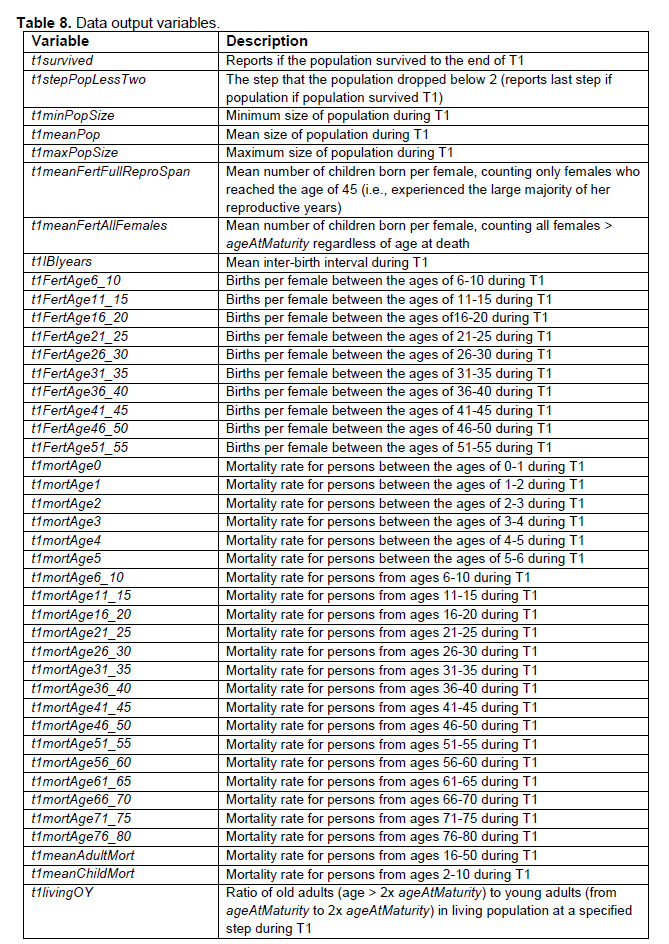
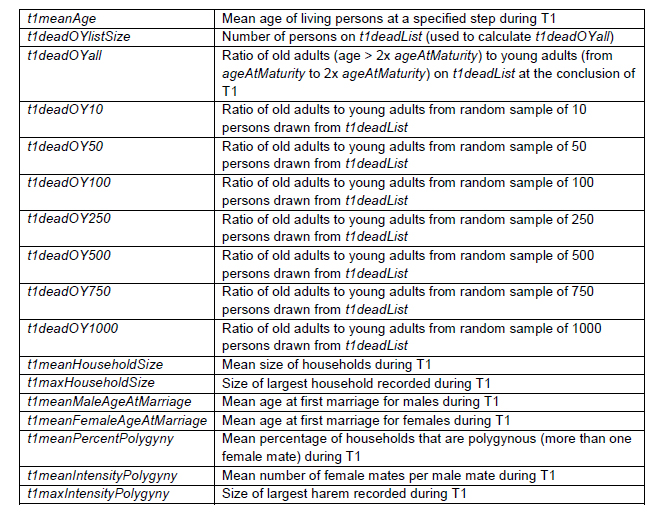
There are numerous variables in the model that are used for storing the information needed to produce summary data outputs at the end of the run. Table 8 summarizes the variables that are calculated as data outputs. The values of many of the parameters that set the conditions of the model (see Table 5) are also reported as data outputs.
Model Structure and Methods
This section describes the methods and inter-relationships between methods that affect the behaviors and interactions of the entities in the model. Methods in the model are initiated and performed by the model or by individual persons. Methods are inter-related through a variety of feedbacks and effects. The major methods of the model are representations of rules governing male-female pair bonds (marriages), reproduction, and mortality.
The parenthetical numeric designations inserted in the narrative descriptions below (and in the comments in the model code) are an effort to help the reader locate relevant sections of code. The designation “Model 12”, for example, means that the method or code being discussed is labeled “12” in the code within the Model.java file. Numbered sections of code are placed in numerical order within each model file. The descriptions provided here are also given in the order they are numbered, although operations in the model are not called in strictly numerical order. Model-level methods are described first, followed by person-level methods.
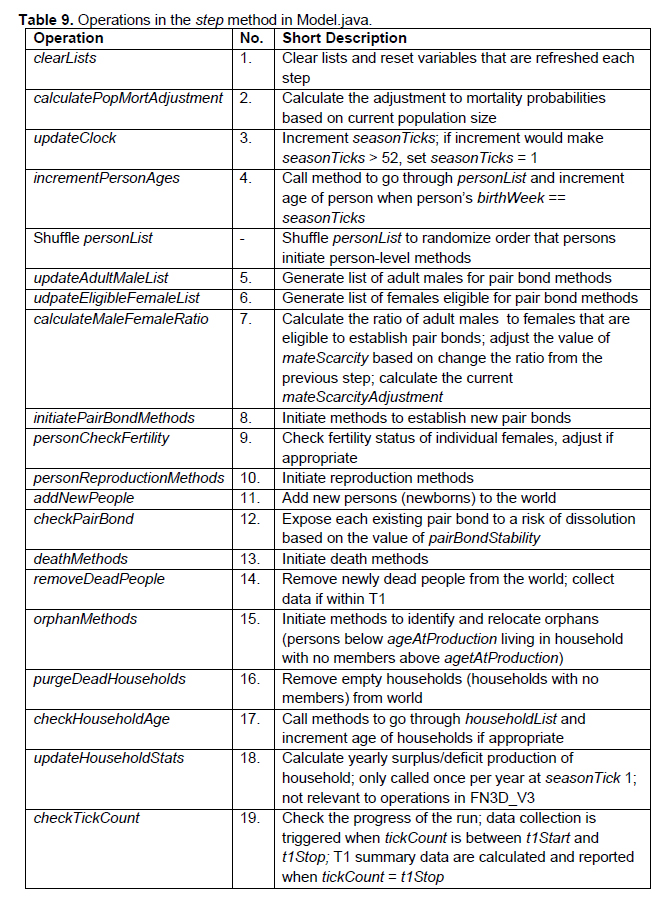
Model-Level Step Method
The step method in Model.java is called at the beginning of every step to initiate a sequence of operations. The order of the operations called by the step method is shown in Table 9.
The parenthetical numeric designations inserted in the narrative descriptions below (and in the comments in the model code) are an effort to help the reader locate relevant sections of code. The designation “Model 12”, for example, means that the method or code being discussed is labeled “12” in the code within the Model.java file. Numbered sections of code are placed in numerical order within each model file. The descriptions provided here are also given in the order they are numbered, although operations in the model are not called in strictly numerical order. Model-level methods are described first, followed by person-level methods.
Model-Level Step Method
The step method in Model.java is called at the beginning of every step to initiate a sequence of operations. The order of the operations called by the step method is shown in Table 9.
Model-Level Method
|
Model 1: Clear Lists
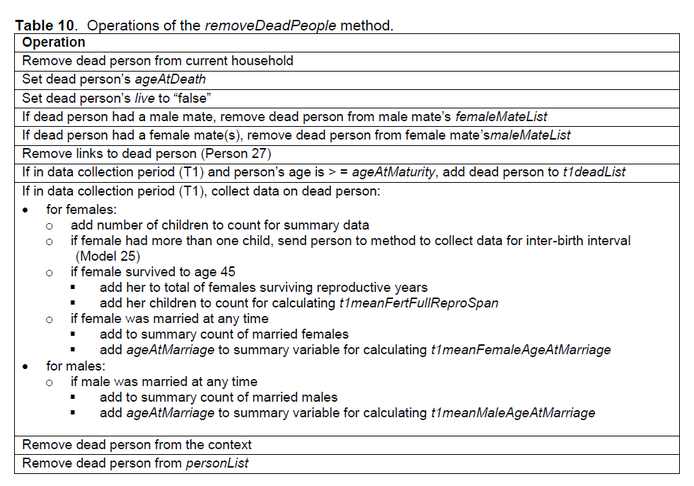
This method clears the lists that are re-generated each step: adultMaleList, eligibleFemaleList, pairBondOrder, addList, and subtractList. Model 2: Calculate Mortality Adjustment Based on Current Population Size Each step, the model adjusts the value of popMortAdjustment by dividing the current population size by the size set by the parameter popMortAdjustPoint and multiplying by the value of the parameter popMortAdjustMult. If the current population is 605, for example, and popMortAdjustPoint = 500 and popMortAdjustMult = 1.5, the value of popMortAdjustment becomes 1.815 (605/500 * 1.5). This value is used to adjust the mortality probabilities when the death methods are called (Model 13). Model 3: Update Clock This method increments the “seasonal clock”, adding 1 to the value of seasonTicks. If this causes the value of seasonTicks to exceed the value of the parameter stepsPerYear, the value of seasonTicks is set to 1. In all cases in the FN3D_V3 model, each season tick represents 1 week. There are 52 season ticks in one year. Model 4: Increment Person Ages This method cycles through the personList, checking to see if the current value of seasonTicks is equivalent to a person’s birthWeek. If the two match (i.e., the person was born during the current week of the year), the person-level method incrementAge is called (Person 1). Model 5: Update Adult Male List The model cycles through the personList and adds all males of age greater than ageAtMaturity to the adultMaleList. Model 6: Update Eligible Female List The model cycles through the personList to identify females who are eligible to establish a new pair bond. Females with age greater than ageAtMaturity who have no current male mate and are not pregnant are added to the eligibleFemaleList. The list is shuffled to produce a random ordering. Model 7: Calculate Male Female Ratio This method calculates the current ratio of males eligible to establish a new pair bond (defined as the size of the adultMaleList) to females eligible to establish a new pair bond (defined as the size of the eligibleFemaleList). This variable is named eligibleMaleFemaleRatio. If the eligibleMaleFemaleRatio has increased from the previous step (i.e., eligible females have become relatively more scarce), the value of mateScarcity is increased by a random double between 0 and 1. If the eligibleMaleFemaleRatio has decreased from the previous step (i.e., eligible females have become relatively less scarce), the value of mateScarcity is decreased by a random double between 0 and 1. If there are no eligible females, the value of mateScarcity is increased by a random double between 0 and 1. If there are no eligible males, the value of mateScarcity is decreased by a random double between 0 and 1. If the change in the value of mateScarcity results in a value that exceeds the upper and lower limits set by the parameters upperMSLimit and lowerMSlimit, the value of mateScarcity is constrained to be within those limits. The variable mateScarcityAdjustment is then calculated by dividing mateScarcity by upperMSLimit. This will return a number between -1 and +1. Model 8: Initiate Pair Bond Methods This method cycles through the adultMaleList and places each male on the list on the pairBondOrder list. The order of persons on the pairBondOrder list is then randomly shuffled. The method then cycles through the pairBondOrder list, calling beginPersonPairBondMethods (Person 2) for each person on the list. [In future versions of the model, the pairBondOrder list could be used to hold a non-random order in which males would initiate pair bond methods (e.g., based on current number of female mates, age, number of social links, etc.)]. Model 9: Check Fertility This method cycles through the personList to identify females whose age >= ageAtMaturity. The checkFertility method (Person 16) is called for those persons. Model 10: Start Reproduction Methods This method cycles through the personList to identify persons who are eligible for the person-level reproduction methods or are already pregnant. The person-level pregnancy method (Person 17) is called for females who are older than ageAtMaturity, have a current male mate, are fertile, and are not pregnant. If a female is pregnant but has reached the end of her pregnancy (i.e., pregnancyWeeks == gestationWeeks), the birth method (Person 19) is called. If a female is pregnant but has not reached the end of her pregnancy, her count of pregnancy weeks (tracked by the variable pregnancyWeeks) is incremented. Model 11: Add New People This method adds each newborn person on the addList to the personList. If the person was born after the start of the data collection period (T1) but long enough before the end of T1 that the person will die within T1 (t1Stop – maxAge – 1), the person is sent to the countLivingPerson method (Model 20) to be tallied for purposes of calculating the age-specific mortality rates experienced by the population during T1. Model 12: Check Pair Bonds This model exposes each existing pair bond to risk of dissolution governed by the value of the parameter pairBondStability. The parameter pairBondStability can vary between 0 and 1. The method cycles through the personList to identify females who have a current male mate. For each of these females, the model generates a random number between 0 and 1. If the number is greater than the value of pairBondStability, the female calls the dissolvePairBond method (Person 24). If the value is 1, all pair bonds are stable and do not dissolve unless one of the mates dies. Model 13: Death Methods This method cycles through the personList and exposes each person to a risk of death through the person-level death method (Person 25). Model 14: Remove Dead People This method cycles through the subtractList and performs operations to remove dead people from the world and collect data about them. These operations are summarized in Table 10. |
|
Model 15: Orphan Methods
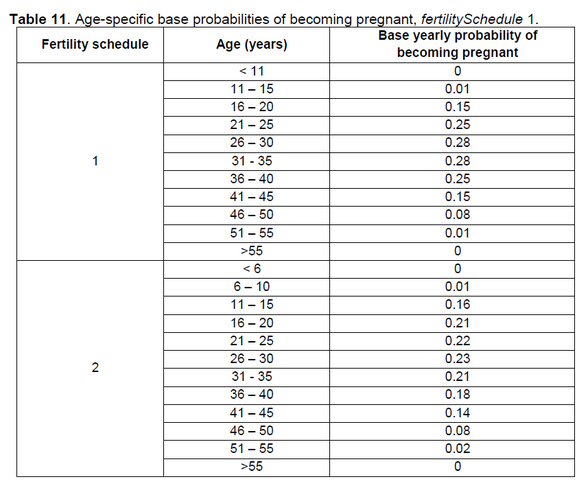
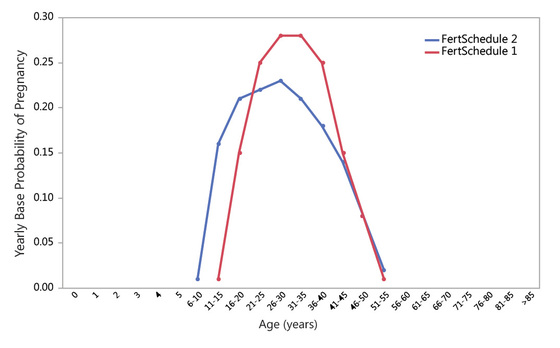
This method cycles through the personList and calls a person-level method to check the orphan status of each person (Person 29). If a person is an orphan, the model sends the person to the reHouseOrphan method (Person 30). Model 16: Purge Dead Households This method identifies households that no longer have any members and removes them from the model’s householdList and removes them from the context. Model 17: Check Household Age This method cycles through the householdList, checking to see if the current value of seasonTicks is equivalent to a household’s birthWeek. If the two match (i.e., the household was created during the current week of the year), the age of the household (tracked by the household variable year) is incremented. Model 18: Update Household Stats This method is only called once per year (when seasonTicks == 1). The method cycles through the householdList, sending each household to the household-level calculateSurplusForYear method (Household 1). Model 19: Check Tick Count The final method of the step method contains operations for triggering data collection and reporting. If the model run is within the data collection period (T1), the collectSummaryData method (Model 26) is called. If the population is higher than at any step previously in T1, population size is recorded as maxPopSize. If the population is lower than at any step previously in T1, population size is recorded as minPopSize. The model is configured to collect data on the living population halfway through T1, calling the reportDemographicData method (Model 27), the calculateLivingOY method (Model 28), and the calculateMeanAgeT1 method (Model 29). If the model run is at the final step of T1 (t1stop), methods are called to record the data accumulated during T1 (Model 30) and report those data (Model 31). Model 20: Count Living Person This method is called when a person’s age is incremented (Person 1) or a new person is added to the world (Model 11) during the data collection period (T1). The model determines the age of the person and increments the tally if the person is entering one of the 5-year age categories. If a person is age 26, for example, the variable numAge26_30 is incremented. This variable is not incremented when the person turns 27. A separate tally is kept for females. These tallies provide the basis for calculating age-specific mortality and fertility rates (see Model 30). Model 21: Get Base Fertility This method obtains the yearly probability of becoming pregnant by consulting the appropriate fertilitySchedule and multiplying the age-specific fertility rate in that schedule by the value of the parameter fertilityMultiplier. In this iteration of FN3D_V3, there are two fertility schedules. The values for fertilitySchedule 1 and fertilitySchedule 2 are shown in Table 11. Fertility schedule 2 (not yet the subject of experimentation) is meant to represent a chimpanzee-like pattern of age-specific fertility. Age-specific fertility probabilities are shown graphically in Figure 4. |
|
Model 22: Create Child
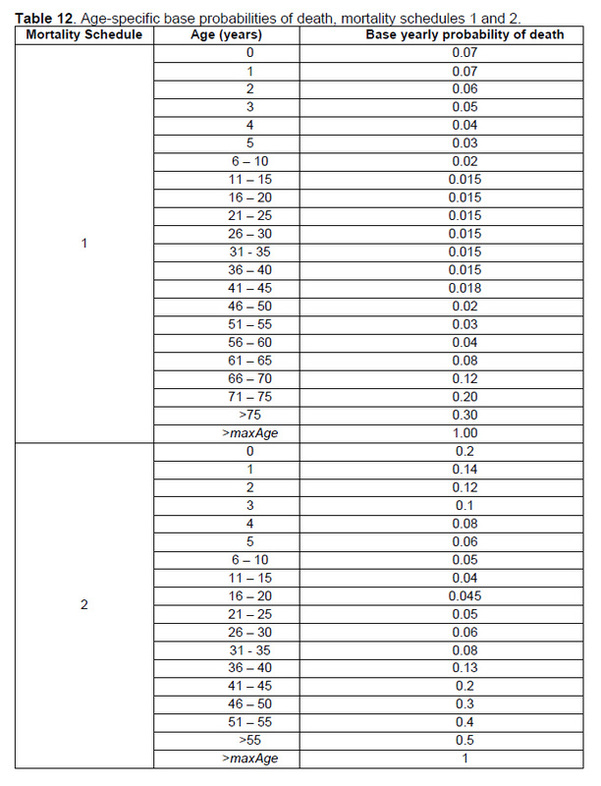
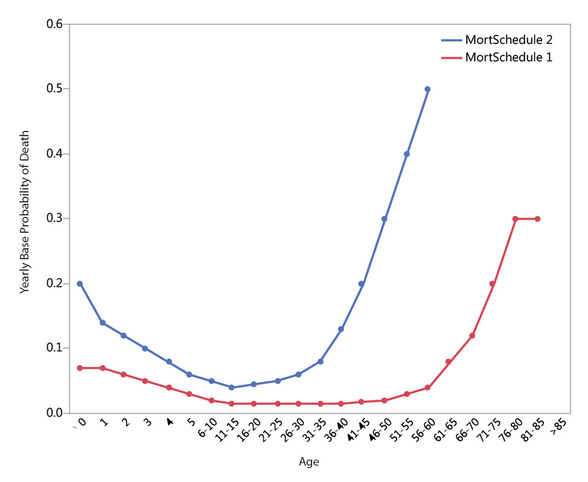
This method is called by the person-level birth method (Person 15) to create a new person (child) of age 0 and random sex. The child’s birthStep is recorded as the current step. The child’s birthWeek is recorded as the current value of seasonTicks. A random number between 1 and numMarriageDivisions is generated for the child’s marriageDivision. The child is added to the addList. During the data collection period (T1), this method tallies births by females of specific age categories (5 year increments). These tallies allow the model to calculate the age-specific fertility rates experienced by the population. The child is returned to the giveBirth method (Person 19). Model 23: Get Base Mortality This method obtains the yearly probability of death by consulting the appropriate mortalitySchedule and multiplying the age-specific mortality rate in that schedule by the value of the parameter mortalityMultiplier. In this iteration of FN3D_V3, there are two mortality schedules. The values for mortality schedules 1 and 2 are shown in Table 12. Mortality schedule 2 (not yet the subject of experimentation) is meant to represent a chimpanzee-like pattern of age-specific mortality. Age-specific mortality probabilities are shown graphically in Figure 5. |
|
Model 24: Kill Person
This method places a person who has died on the model-level subtractList. Model 25: Count for Inter-Birth Interval This method is called upon the death (during T1) of a female who experienced multiple live births during her lifespan. The method calculates the interval of time (in years) between successive births by cycling through the female’s childList and comparing the values of birthStep for successive children on the list. If the first child was born on step 6000 and the second child was born on step 6200, for example, the inter-birth interval between the first and second children would be calculated as (6200 – 6000) / 52 = 3.85 years. The intervals between each pair of successive births are calculated and added to the summary total to be used in calculating t1IBIyears. Model 26: Collect Summary Data This method is called each step during the data collection period (T1) to record data that are used to calculate summary measures reported at the end of T1. The operations of the collectSummaryData method are summarized in Table 13. |
|
Model 27: Report Demographic Data
This method prints a file containing data about each living person (e.g., identification number, sex, age, size of person’s personLinkList, number of kinLinks, number of female mates – other attributes can be added). The method produces an output file named “DemographicData.txt”. The method is called from the checkTickCount method (Model 19) and can be switched on/off there. Model 28: Calculate Living OY Ratio This method calculates the ratio of old adults to young adults in the living population. The method cycles through the personList and checks each person’s age. If a person is older than or equal to ageAtMaturity but not twice the ageAtMaturity, the person is counted as a “young adult.” If a person is older than or equal to twice the ageAtMaturity, the person is counted as an “old adult.” The value of livingOY is calculated as the number of old adults divided by the number of young adults. This variable is reported in the final summary data file (Model 31). Model 29: Calculate Mean Age of Population This method calculates the mean age of the living population by cycling through the personList, summing the ages of all living persons, and dividing by the population size. The calculated value is stored as t1meanAge and reported in the final summary data file (Model 31). Model 30: Record T1 Data This method records the set values of parameters during T1 and calculates values of summary variables from the data collected during T1. Summary variables were listed in Table 8. Age-specific fertility rates (e.g., t1fertAge26_30) are calculated by dividing the total number of births experienced by females in that age category (see Model 22: createChild) by the number of females that enter that age category (see Model 20: countLivingPerson). The fertility rate experienced by females age 26 to 30, for example, is calculated as: t1fertAge26_30 = numBirthsAge26_30 / numFemalesAge26_30 / 5 The number of births per female is divided by 5 to obtain the yearly fertility rate over the 5-year period. Age-specific mortality rates (e.g., t1mortAge16_20) are calculated by first finding the difference between the number of persons that entered an age category and the number of persons that entered the next age category. For example, if the variable numAge16_20 has a value of 1000 and the variable numAge21_25 has a value of 900, 100 people died between after turning 16 but before turning 21. The total number of deaths is divided by the number that entered the lower age bracket and divided by 5 to obtain the yearly mortality rate experienced by that subset of the population: 100 / 1000 / 5 = 0.02 The overall mean adult mortality rate (t1meanAdultMort) is calculated by averaging the age-specific mortality rates for persons from ages 16 to 50. The mean child mortality rate (t1meanChildMort) is calculated by averaging the age-specific mortality rates for persons between the ages of 2 and 10. he method to calculate the OY ratios of samples of the dead population (Model 31) is called. Model 31: Report Summary Data This method prints a file containing the parameter settings from the model run and summary data from T1. The method produces an output file named “SummaryData.txt”. The ordering of data can be obtained from the code. Model 32: Calculate Dead OY Ratio This method calculates the ratio of old adults to young adults (the OY ratio) in samples of the dead population. A “young adult” is defined as a person whose age is greater than or equal to ageAtMaturity but less than twice ageAtMaturity. An “old adult” is defined as a person whose age is greater than or equal two twice ageAtMaturity. This method first calculates the OY ratio based on all the persons on the t1deadList (all adult persons that died during T1). The method cycles through the list and checks the age of each person on the list. If the person is a “young adult”, the count of young adults is incremented. If the person is an “old adult,” the count of “old adults” is incremented. The OY ratio of the entire assemblage of dead persons (t1deadOYall) is calculated by dividing the count of old adults by the count of young adults. The method then calculates the OY ratio for random samples of varying size drawn from the t1deadList. The method is currently configured to calculate the OY ratio for samples of size 10, 100, 250, 500, 750, and 1000. The procedure for a sample size of 100 will be used as an illustration. The method first checks to see if the size of t1deadList >100. If so, the method cycles through the t1deadList and sets the value of each person’s usedForOY to “false.” The method then randomly draws a person from the t1deadList. If the randomly drawn person can be counted as a “young adult” or “old adult”, the appropriate count is incremented and the value of the variable numFound is incrememented. The value of usedForOY for the person is set to “true” so that the person cannot be counted by the method again for the sample of 100. The method then randomly draws another person from the t1deadList, checks the value of usedForOY, and increments the appropriate count (young adult or old adult) based on the person’s age at death. The method continues randomly drawing persons until a sample of 100 has been collected. The method then calculates and records the OY ratio of the sample (t1deadOY100). |
Person-Level Methods
|
Person 1: Increment Age
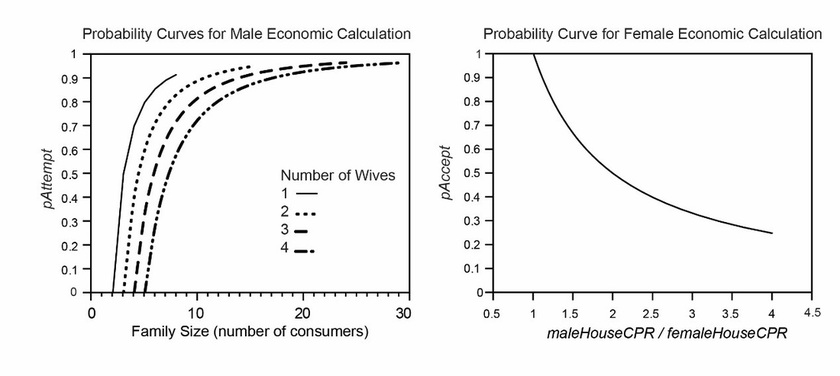
This method adds 1 to the value of age stored by each person. If the person is a female and age == ageAtMaturity, her fertility status is set to “true.” This method then checks to see if the person was born after the start of the T1 data recording period (birthStep >= t1Start) but not so late in the T1 period that the person may not die before the end of T1 (birthStep > (t1Stop – maxAge)). If so, the person is sent back to the model to be tallied as a living person for purposes of calculating mortality (Model 20). Person 2: Begin Person Pair Bond Methods This is the beginning of the person-level pair bond methods. It is called sequentially for each male on the pairBondOrder list. If the male has no current mate, he calls the findMate method (Person 5). If the male already has a mate and polygyny is allowed (i.e., pairBondMode == 2), he calls the evaluatePairBondEconomics method (Person 3). Note that all single adult males will go straight to the findMate method regardless of the value of pairBondMode. Person 3: Evaluate Pair Bond Economics This method is only called by males who already have at least one female mate. If this method is called, the male will evaluate the economic benefit of adding an additional mate to his existing household. The economic benefit (econBenefit) of adding another mate is calculated as the difference between the dependency ratio in his current family (curCPR) and the dependency ratio if he adds another mate (condCPR) as a percentage of his current dependency ratio: econBenefit = (curCPR – condCPR) / curCPR The addition of a single adult to a household will always lower the dependency ratio if it is above 1: this equation will always yield a positive number. Figure 6 (left) shows the results of this equation under circumstances of varying family size and a varying number of existing female mates. This simple calculation is intended to capture two key aspects of the economics of polygyny: (1) wives are more likely to be added when the addition is of greater economic benefit; and (2) as family size increases, each additional wife has progressively less impact on the dependency ratio, all other things being equal. |
|
The base probability that a male will attempt to add another mate (pAttempt) is calculated as:
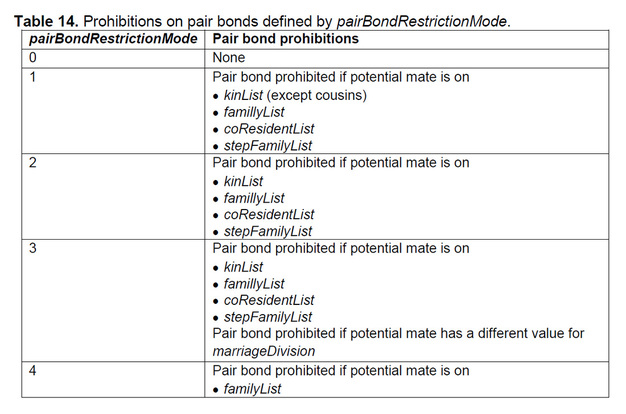
pAttempt = 1 - ((1 - econBenefit) * econWeight) where econWeight is the same as the value of the parameter householdEconWeight set in the model. Note that if the value of householdEconWeight is set to 0, the dependency ratio plays no role in whether or not a male will attempt to add an additional mate to his household: the value of pAttempt will be calculated as 1. If the model is set to alter the probabilities of establishing new pair bonds based on the scarcity of possible mates (i.e., mateScarcityAdjustmentSwitch == true), the value of pAttempt is sent to the eligibleFemaleScarcityAdjustment method (Person 4) to be adjusted. If mateScarcityAdjustmentSwitch == false, mate scarcity plays no role in a decision to attempt to add another mate. The final value of pAttempt is compared to a random number between 0 and 1. If the number is < pAttempt, the findMate method (Person 5) is called. If the number is > pAttempt, no additional mate is sought and the pair bond methods end for the person. Person 4: Eligible Female Scarcity Adjustment This method takes the value of pAttempt calculated in evaluatePairBondEconomics (Person 3) and applies an adjustment based on the scarcity of female mates. The method retrieves the current value of mateScarcityAdjustment calculated earlier in the step (Model 7). The value of mateScarcityAdjustment will always be between -1 and +1. If the value of mateScarcityAdjustment is greater than 0 (i.e., there has been an overall trend of scarcity of potential female mates), pAttempt is adjusted by adding the value of (pAttempt * mateScarcityAdjustment). If mateScarcity is at its maximum positive limit (+1), this will result in doubling the value of pAttempt (i.e., it will be twice as likely that a male will seek an additional mate). Note that pAttempt is not adjusted if mateScarcityAdjustment < 0. Following adjustment, the new value of pAttempt is returned to the evaluatePairBondEconomics method. Person 5: Find Mate This method cycles through the model’s eligibleFemaleList to select a female as a potential mate. The method checks to confirm the selected female is alive, has no current mates, and is not pregnant. The selected female is sent to the attemptPairBond method (Person 6). Person 6: Attempt Pair Bond This method calls additional methods to ask three questions: 1. Would establishing a pair bond between the male and female violate an incest prohibition (Person 7)? 2. Does the male reject the pair bond because it would create an economically difficult household situation (Person 8)? 3. Does the female decline the pair bond based on the difference between her current economic situation and the situation she would be moving into (Person 9)? If the answer to any of these questions is “yes,” the pair bond methods end. If the answer to all of these questions is “no,” the createPairBond method (Person 11) is called. Person 7: Check for Incest Prohibition This method checks to see if the pair bond would violate any incest prohibitions. Restrictions on pair bonds are specified by the value of the model-level parameter pairBondRestrictionMode (Table 14). If the pair bond is prohibited, the pair bond methods end. If the pair bond is not prohibited, the method returns a “go ahead” result to the attemptPairBond method (Person 6). |
|
Person 8: Economic Liability Check
This method evaluates, from the male’s perspective, the economics of establishing a household with the particular female (and her dependents, if any) or adding her (and her dependents, if any) to an existing household. The evaluatePairBondEconomics method (Person 3) discussed above evaluated the “generic” economics of adding a female mate to a particular existing household. This method, in contrast, evaluates the economics of partnering with a particular female and her existing dependents. Eligible females may have existing dependents (but no current male mate) if they were part of a household where the male mate died. When the adult male of a household dies, any children less than ageAtMaturity will remain with their mother and become part of a household she joins or establishes with a new mate. If the female has no dependents, the method returns a “go ahead” result. If the female has dependents, the model calculates the dependency ratio of the household that would contain the male (and any existing co-wives and children) and the female and her existing dependents (condCP). If the dependency ratio of the household would be below the value of the model-level parameter sustainableCP, the method returns a “go ahead” result. If the dependency ratio of the male’s household would be above the value of sustainableCP, the base probability that the pair bond will be accepted (pAccept) is calculated as: pAccept = (condCP – sustainableCP) / sustainableCP In other words, the probability of accepting the pair bond is inversely proportional to the degree to which the “new” household would exceed the dependency ratio defined as sustainable. This base probability is subject to modification by the model-level parameter householdEconWeight. This parameter specifies the strength of the role that the dependency ratio plays in economically-sensitive calculations. The following calculations are performed: pReject = 1 – pAccept pReject = pReject * householdEconWeight pAccept = 1 - pReject When householdEconWeight == 0, the value of pAccept will become 1. When householdEconWeight == 1, the value of pAccept stays the same as originally calculated. The final value of pAccept is compared to a random number between 0 and 1. If the number is < pAccept, the method returns a “go ahead” result to the attemptPairBond method (Person 6). Person 9: Calculate Female Side Economics This method evaluates, from the female’s perspective, how accepting a pair bond with the male would affect her economic situation. It is based on the idea that a female is less likely to enter into a pair bond when it would entail a relative increase in her work load. The method first calculates the dependency ratio of the current household that the female is in (femaleHouseCPR). If the female was previously married, her current household may contain dependents from a previous marriage where the male has died. If the female has not been previously married, her current household is that of her parents. The base probability that the female will accept the pair bond (pAccept) is then calculated as: pAccept = 1 / (maleHouseCPR / femaleHouseCPR) where maleHouseCPR is what the dependency ratio of the male household would be after the female (and any of her dependents) joined the household. The results of this formula are illustrated in Figure 4 (right). There is a base 50 percent probability that a female will enter into a household that will put her in a situation where the dependency ratio is twice as high as in her current situation. This base probability is subject to modification by the model-level parameter householdEconWeight. This parameter specifies the strength of the role that the dependency ratio plays in economically-sensitive calculations. The following calculations are performed: pReject = 1 – pAccept pReject = pReject * householdEconWeight pAccept = 1 - pReject When householdEconWeight == 0, the value of pAccept will become 1. When householdEconWeight == 1, the value of pAccept stays the same as originally calculated. If the model is set to alter the probabilities of establishing new pair bonds based on the scarcity of possible mates (i.e., mateScarcityAdjustmentSwitch == true), the value of pAttempt is sent to the eligibleMaleScarcityAdjustment method (Person 10) to be adjusted. If mateScarcityAdjustmentSwitch == false, mate scarcity plays no role in a decision to attempt to add another mate. The final value of pAccept is compared to a random number between 0 and 1. If the number is < pAccept, the method returns a “go ahead” result to the attemptPairBond method (Person 6). Person 10: Eligible Male Scarcity Adjustment This method takes the value of pAccept calculated in calcFemaleEconomics (Person 9) and applies an adjustment based on the scarcity of male mates. The method retrieves the current value of mateScarcityAdjustment calculated earlier in the step (Model 7). The value of mateScarcityAdjustment will always be between -1 and +1. If the value of mateScarcityAdjustment is is less than 0 (i.e., there has been an overall trend of scarcity of potential male mates), pAccept is adjusted by adding the value of (pAccept * mateScarcityAdjustment * -1). Because mateScarcityAdjustment will be a negative number in this instance, this will result in increasing the value of pAccept. If mateScarcity is at its maximum lower limit (-1), the value of pAccept will be doubled (i.e., it will be twice as likely that a female will accept a pair bond that puts her in a worse economic situation than she is presently in). Note that pAccept is not adjusted if mateScarcityAdjustment > 0. Following adjustment, the new value of pAccept is returned to the calcFemaleEconomics method. Person 11: Create Pair Bond This method establishes a new pair bond between a male and a female. The operations in this method are summarized in Table 15. This method concludes the pair bond methods. |
|
Person 12: Identify In-Laws
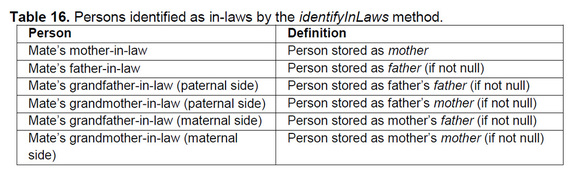
This method is called alternately by the male and female when a pair bond is established. It identifies and create pairs of social links with persons who are now related to the person through marriage. When an in-law is identified, he/she is added to the person’s kinList and, in turn, adds the person to the in-law’s kinList. This happens regardless of whether the in-law is still living. A pair of links is created with each living in-law: one link from the person to the in-law, and another link from the in-law to the person. Table 16 lists the persons identified as in-laws by this method. |
|
Person 13: Identify Step-Children
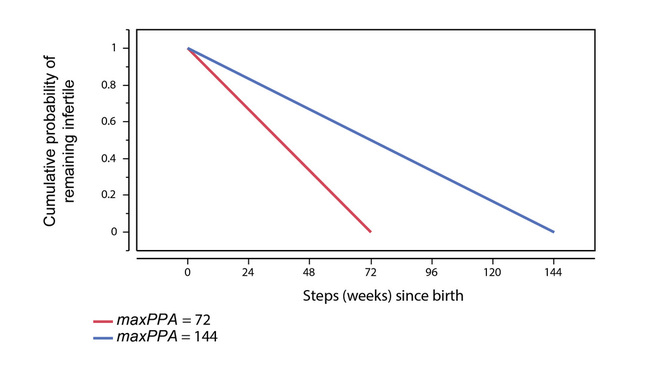
This method is called alternately by the male and the female when a pair bond is established. It identifies and creates pairs of social links with a mate’s living children, checking to make sure those children are not the person’s biological offspring (this is possible in cases where pair bonds are not stable). A pair of kin links is created between the person and each non-biological child. Person 14: Identify Co-Residents This method is called to identify and create pairs of social links between any otherwise unrelated persons residing in the same household. It is called when a person enters a new household through birth, marriage, or as an orphan. The method cycles through current members of the household and checks them against the person’s coResidentList. If the household co-resident is not on the person’s coResidentList, the household co-resident is added to the list (and vice versa). If no link is found with a member of the household (i.e., the person is not family or kin), the method creates a pair of links: one from the new person to the co-resident and one from the co-resident to the new person. Person 15: Switch Children to New Household This method is called when a new pair bond is established to move any existing children of the female to the new household. The method cycles through the childList of the female and identifies any offspring that were living in the same household as the female. Those offspring are removed from the old household and placed in the female’s new household. The identifyCoResidents method (Person 14) is called for each child that is moved. Person 16: Check Fertility This method checks the fertility status of mature females and adjusts that status if appropriate. This method can only change fertile from “false” to “true.” Changing fertile from “true” to “false” occurs during the reproduction methods when a female becomes pregnant (Person 17). If a female is currently fertile, the method ends. If a female is not fertile (fertile == false) and is not pregnant (pregnancyWeeks == 0), the model first checks to see if she has a living, un-weaned child. If so, the model checks the value of the parameter ageAtWeaningWeight. This parameter specifies if weaning age is relevant to determining a female’s fertility status. If ageAtWeaningWeight == 0 (weaning age is irrelevant), the model calculates the probability (pFertile) that the female’s fertility status will change to “true” using the following calculation: pFertile = 1 / maxPPA The parameter maxPPA specifies the maximum duration of post-partum amenorrhea (infertility following childbirth) in weeks. The calculation above represents the return of fertility after childbirth as a linear, time-dependent phenomenon. The probability that fertility will return stays constant each week following birth, resulting a linear increase in the cumulative probability that a female will return to a fertile state. Figure 7 shows the time-dependent decrease in infertility following birth for cases where maxPPA is 72 (18 months) and 144 (36 months). The value of pFertile is compared to a random number between 0 and 1. If the number is lower than pFertile, the female’s fertility status is set to “true” and stepsPPA is set to 0. The variable stepsPPA counts the number of steps that a female has been infertile following childbirth. If the number is higher than pFertile, the female’s fertility status remains “false” and the value of stepsPPA is increased by 1. If the value of stepsPPA > maxPPA, fertile is set to “true” and stepsPPA is set to 0. If the female is not pregnant and does not have a living, un-weaned child, fertile is set to “true” and stepsPPA is set to 0. |
|
Person 17: Pregnancy
This method determines if a female will become pregnant. The method first sends the female’s age to the getBaseFertility method in the model (Model 21). That method returns the base yearly probability of becoming pregnant. The yearly probability of pregnancy is divided by the number of steps per year (52) in order to calculate the weekly probability of pregnancy (pPregnancy). A random number between 0 and 1 is generated. If the number is higher than pPregnancy, the female does not become pregnant and the reproduction methods end. If the number is lower than pPregnancy, the avoidPregnancy method (Person 18) is called. If that method returns a negative result (i.e., pregnancy is not avoided) the female becomes pregnant. The female’s count of pregnancyWeeks is set to 1, fertile is set to “false”, and stepsPPA is set to 0. Person 18: Avoid Pregnancy This method provides a mechanism for a pregnancy to be avoided because of the dependency ratio of the household. It is called when a female becomes pregnant (Person 17). Whether or not the method is operation is determined by the model-level parameter avoidanceOn. If avoidanceOn is set to “false,” the method ends. If avoidanceOn is “true,” the method calculates what the dependency ratio of the household would be if another child was added (condHouseholdCP). If condHouseholdCP is higher than the value of sustainableCP stored by the model, the method calculates the base probability of avoiding pregnancy (pAvoid) as: pAvoid = ((condHousehodCP – sustainableCP) / sustainableCP) The calculated value of pAvoid is then multiplied by the value of the parameter householdEconWeight, which can vary between 0 and 1. As in other methods, this adjusts how heavily the dependency ratio affects economic decisions. If householdEconWeight is 0, pregnancy will never be avoided. If householdEconWeight is 1, the value of pAvoid will remain the same as calculated. The value of pAvoid is compared to a random number between 0 and 1. If the number is less than pAvoid, the pregnancy will be avoided and the reproduction methods ended. If the number is greater than pAvoid, the pregnancy will not be avoided. The result is returned to the pregnancy method (Person 17). Person 19: Give Birth This method creates a new person (child) by calling the model-level createChild method (Model 22). If the female has a current living male mate, that male mate is set as the child’s father. The male mate adds the child to his childList. Note that the male mate of the female may not be the biological father of the child: if a male mate dies during the gestation period or if the pair bond is dissolved, the female may have a different male mate by the time she gives birth. The child sets the female as mother, and the female adds the child to her childList. The child is added to the female’s currentHousehold. The child then calls methods to identify and create social links with family members (Person 20), maternal kin (Person 21), and children of siblings (Person 22). If the child has a father, the child calls a method to identify paternal kin (Person 23). Finally, the child calls a method to identify otherwise unrelated household co-residents (Person 14). The child is put into the world of the model and the female’s pregnancyWeeks is set to 0. This concludes the reproduction methods. Person 20: Identify Family Members This method is called by a newborn child to identify and create pairs of social links with persons who are related to the child by descent. When a family member is identified, he/she is added to the child’s familyList and, in turn, adds the child to his/her familyList. This happens regardless of whether the family member is still living. A pair of links is created with each living family member: one link from the child to the family member, and another link from the family member to the child. Table 17 lists the persons identified as family members by this method. |
|
Person 21: Identify Maternal Kin
This method is called by a newborn child to identify and create pairs of social links with persons who are related to the child as maternal aunts, uncles, and cousins. The method begins by cycling through the child’s mother’s siblingList, adding each person on that list to the child’s kinList and adding the child to each of the mother’s sibling’s kinList. If the mother’s sibling is alive, a pair of links is created: one link from the child to the mother’s sibling, and another link from the mother’s sibling to the child. The method cycles through the childList of each of the mother’s siblings to identify cousins, adding each cousin to the newborn child’s cousinList. If the cousin is alive, a pair of links is created: one link from the child to the cousin, and another link from the cousin to the child. Person 22: Identify Sibling Kin This method is called by a newborn child to identify and create pairs of social links with the offspring of the child’s siblings (i.e., nieces and nephews). The method cycles through the childList of each person on the child’s siblingList, adding each niece/nephew to the child’s kinList and adding the child to the kinList of each niece/nephew. If the niece/nephew is alive, a pair of links is created: one link from the child to the niece/nephew, and another link from the niece/nephew to the child. Person 23: Identify Paternal Kin This method is called by a newborn child to identify paternal kin. It is only called if the father of the child is not null. Other than working on the paternal side, the method is identical to the identifyMaternalKin method (Person 17). Person 24: Dissolve Pair Bond This method dissolves a male-female pair bond. The female removes the male from her maleMateList and the male removes the female from his femaleMateList. The links between the male and female are changed to ex-mate links (linkType = 6). The female removes herself from the male’s household and forms a new household. Any children of the female that are still residing with her are moved to the new household with the switchChildrenToNewHousehold method (Person 15). Person 25: Death This method exposes a person to risk of death. The method first sends the person’s age to the model-level getBaseMortality method to obtain the base yearly probability of death (Model 23). The yearly base probability of death is divided by the number of steps per year (52) and multiplied by the current value of popMortAdjustment (see Model 2) in order to calculate the weekly probability of death (pDeath). A random number between 0 and 1 is generated. If the number is less than pDeath, the person is sent to the killPerson method (Model 23). If the number is greater than pDeath but the person is 0 years of age and has not previously been exposed to a risk of infanticide (infanticideRiskExposed == false), the calculateInfanticide method (Person 26) is called. If that method returns a “true” result, the person is sent to the killPerson method (Model 24). Finally, if the person’s age is greater than or equal to maxAge, the person is sent to the killPerson method. Person 26: Calculate Infanticide This method exposes newborns to a risk of infanticide. This risk of death is in an addition to the risk of death that each person is exposed to by the primary death method (Person 25). A newborn is only exposed to a risk of death by infanticide one time. This occurs in the same step as birth. After this exposure, the newborn’s infanticideRiskExposed variable is set to “true” to prevent the newborn from being exposed to infanticide risk again. The infanticide method begins by checking the value of the model-level parameter infanticideOn. If that parameter is set to “false”, there is no infanticide and the method ends. If it is “true,” the method first calculates the probability of infanticide for economic reasons. If the dependency ratio of the household (householdCP) is above the value set for sustainableCP, the base probability of infanticide (pInfanticide) is calculated as: pInfanticide = ((householdCP – sustainableCP) / sustainableCP (Note that this formula is the same as that used to calculate the probability of avoiding pregnancy in the avoidPregnancy method [Person 18]). The calculated value of pInfanticide is then multiplied by the value of the parameter householdEconWeight, which can vary between 0 and 1. As in other methods, this adjusts how heavily the dependency ratio affects economic decisions. If householdEconWeight is 0, infanticide for economic reasons will never occur. If householdEconWeight is 1, the value of pInfanticide will remain the same as calculated. The value of pInfanticide is compared to a random number between 0 and 1. If the number is less than pInfanticide the method returns a “true” result to the death method (Person 25), resulting in the person being sent to the killPerson method (Model 24) method in the model. If there was no infanticide for economic reasons, the newborn is exposed to a risk of non-economic infanticide (i.e., a risk that is independent of the household dependency ratio). The probability of non-economic infanticide is set by the model-level parameter nonEconInfanticideRisk. The value of this parameter can vary between 0 and 1. If it is set to 0, the method ends. If the value of the parameter is greater than 0 (i.e., there is a risk of non-economic infanticide), its value is compared to a random number between 0 and 1. If the number is less than nonEconInfanticideRisk the method returns a “true” result to the death method (Person 25), resulting in the person being sent to the killPerson method (Model 24) method in the model. Person 27: Remove Links to Dead Person This method is called by a dead person from the removeDeadPeople method (Model 14) to remove all social links originating from the dead person. The method cycles through the dead person’s personLinkList and calls the deleteLinkToMe method (Person 28) for each linked person. Each link originating from the dead person is added to a temporary removeLinkList that is created by the method. After the method cycles through the dead person’s personLinkList, it cycles through the removeLinkList and calls a method to remove each link on that list from the model’s linkList. Person 28: Delete Link to Me This method is called from the removeLinkstoMe method (Person 27) to remove a link from a live person to a dead person. The dead person is sent to the method. The live person searches his/her personLinkList until the link to the dead person is found. The link is removed from the personLinkList and sent to the model to be removed from the model’s linkList. Person 29: Check Orphan Status This method checks to see if the person is an “orphan.” An orphan is defined as a person who is below the ageAtProduction set by the model and is not residing in a household with anyone who is above ageAtProduction (i.e., the person is a consumer in a household with no producers). If a person is below the ageAtProduction, this method cycles through the other members of the household to see if anyone in the household is above the ageAtProduction. It there are no producers in the household, the method returns a “true” result to the model-level orphanMethods method (Model 15). Person 30: Re-House Orphan This method is called to place an orphan in a new household. An orphan is defined as a person who is below the ageAtProduction set by the model and is not residing in a household with anyone who is above ageAtProduction. This method seeks to place the orphan in a household that contains at least one person of producer age. The method first cycles through the familyList of the orphan to identify a family member that is alive, above the ageAtProduction, and in a household. If such a family member is located, the orphan is moved to that person’s household. If no suitable family member is located, the orphan searches his/her coResidentList to identify a person that is alive, above the ageAtProduction, and in a household. If such a person is located, the orphan is moved to that person’s household. If no suitable person is located on the orphan’s coResidentList, the orphan then cycles through his/her personLinkList to identify any linked person that is alive, above the ageAtProduction, and in a household. If such a person is located, the orphan is moved to that person’s household. After a the orphan moves to his/her new household, the identifyCoResidents method (Person 14) is called to identify and create social links with members of the household to whom the former orphan is not already linked. No provision is made for what to do with an orphan in the very unlikely event that no suitable household is located. |
Household-Level Methods
|
Household 1: Calculate Surplus for Year
This method calculates the current surplus/deficit of the household based on the dependency ratio. The method first calculates the current dependency ratio (currentCPRatio). If the current dependency ratio of the household is higher than at any previous time, the current value is stored as peakCPRatio. If the household is larger (has more members) than at any previous time, the current size of the household is stored as peakSize. If the household has more producers than at any previous time, the number of producers is stored as peakProducers. If the household has more non-producers than at any previous time, the number of non-producers is stored as peakDependents. If there are more female mates in the household than at any previous time, the number of female mates is stored as peakFemaleMates. The method then calculates the current productive capacities of the household (currentSurplus). Note that while the current dependency ratio of a household plays a role in many economic calculations in this version of the FN3D_V2 model, cumulative productive surpluses or deficits do not (as in the FamilyNet model used by White 2013). Economic surplus/deficit will be relevant to future versions of the model. The current productive capacity of the household is calculated as: currentSurplus = (currentNumProducers * 1.75) – currentSize This equation assumes that each producer has 1.75 “units” of productive capacity, while each member of the household consumes 1 unit. |
Model Startup
The ForagerNet3Builder.java file is called when a model run is initiated. This method creates a new instance of model, sets the space and grid, and creates the people to populate the world. Although the model takes place in a grid, there is no spatial component to any of the methods in this version.
The createPeople method creates a population of the size specified by the parameter initNumPersons. As currently configured, this method creates a population of persons of random sex with random ages between ageAtMaturity and 20. The model assigns random marriage divisions between 1 and the value of numMarriageDivisions and a random birthWeek between 1 and 52. Each new person is added to the personList and put into the world.
The createPeople method creates a population of the size specified by the parameter initNumPersons. As currently configured, this method creates a population of persons of random sex with random ages between ageAtMaturity and 20. The model assigns random marriage divisions between 1 and the value of numMarriageDivisions and a random birthWeek between 1 and 52. Each new person is added to the personList and put into the world.
References
Gilbert, Nigel. 2008. Agent-Based Models. Quantitative Applications in the Social Sciences 153. Sage Publications, Thousand Oaks, California.
White, Andrew A. 2016. The Sensitivity of Demographic Characteristics to the Strength of the Population Stabilizing Mechanism in a Model Hunter-Gatherer System. In Uncertainty and Sensitivity Analysis in Archaeological Computational Modeling, edited by Marieka Brouwer Burg, Hans Peeters, and William Lovis, pp. 113-130. Switzerland: Springer International.
White, Andrew A. 2014. "ForagerNet3_Demography_V2" (Version 1). CoMSES Computational Model Library. Retrieved from: https://www.openabm.org/model/4087/version/1
White, Andrew A. 2012. The Social Networks of Early Hunter-Gatherers in Midcontinental North America. Unpublished Ph.D. Dissertation, Department of Anthropology, University of Michigan, Ann Arbor.
White, Andrew A. 2016. The Sensitivity of Demographic Characteristics to the Strength of the Population Stabilizing Mechanism in a Model Hunter-Gatherer System. In Uncertainty and Sensitivity Analysis in Archaeological Computational Modeling, edited by Marieka Brouwer Burg, Hans Peeters, and William Lovis, pp. 113-130. Switzerland: Springer International.
White, Andrew A. 2014. "ForagerNet3_Demography_V2" (Version 1). CoMSES Computational Model Library. Retrieved from: https://www.openabm.org/model/4087/version/1
White, Andrew A. 2012. The Social Networks of Early Hunter-Gatherers in Midcontinental North America. Unpublished Ph.D. Dissertation, Department of Anthropology, University of Michigan, Ann Arbor.